API Documentation¶
plfit Module¶
numpy/matplotlib version of plfit.py¶
A power-law distribution fitter based on code by Aaron Clauset. It can use fortran, cython, or numpy-based power-law fitting ‘backends’. Fortran’s fastest.
Requires pylab (matplotlib), which requires numpy
Example very simple use:
from plfit import plfit
MyPL = plfit(mydata)
MyPL.plotpdf(log=True)
- plfit.plfit.alpha_gen(x)[source]¶
Create a mappable function alpha to apply to each xmin in a list of xmins. This is essentially the slow version of fplfit/cplfit, though I bet it could be speeded up with a clever use of parellel_map. Not intended to be used by users.
Docstring for the generated alpha function:
Given a sorted data set and a minimum, returns power law MLE fit data is passed as a keyword parameter so that it can be vectorized If there is only one element, return alpha=0
- plfit.plfit.discrete_alpha_mle(data, xmin)[source]¶
Equation B.17 of Clauset et al 2009
The Maximum Likelihood Estimator of the “scaling parameter” alpha in the discrete case is similar to that in the continuous case
- plfit.plfit.discrete_best_alpha(data, alpharangemults=(0.9, 1.1), n_alpha=201, approximate=True, verbose=True)[source]¶
Use the maximum L to determine the most likely value of alpha
- alpharangemults [ 2-tuple ]
- Pair of values indicating multiplicative factors above and below the approximate alpha from the MLE alpha to use when determining the “exact” alpha (by directly maximizing the likelihood function)
- plfit.plfit.discrete_ksD(data, xmin, alpha)[source]¶
given a sorted data set, a minimum, and an alpha, returns the power law ks-test D value w/data
The returned value is the “D” parameter in the ks test
(this is implemented differently from the continuous version because there are potentially multiple identical points that need comparison to the power law)
- plfit.plfit.discrete_likelihood(data, xmin, alpha)[source]¶
Equation B.8 in Clauset
Given a data set, an xmin value, and an alpha “scaling parameter”, computes the log-likelihood (the value to be maximized)
- plfit.plfit.discrete_likelihood_vector(data, xmin, alpharange=(1.5, 3.5), n_alpha=201)[source]¶
Compute the likelihood for all “scaling parameters” in the range (alpharange) for a given xmin. This is only part of the discrete value likelihood maximization problem as described in Clauset et al (Equation B.8)
- alpharange [ 2-tuple ]
- Two floats specifying the upper and lower limits of the power law alpha to test
- plfit.plfit.discrete_max_likelihood(data, xmin, alpharange=(1.5, 3.5), n_alpha=201)[source]¶
Returns the argument of the max of the likelihood of the data given an input xmin
- plfit.plfit.discrete_max_likelihood_arg(data, xmin, alpharange=(1.5, 3.5), n_alpha=201)[source]¶
Returns the argument of the max of the likelihood of the data given an input xmin
- plfit.plfit.kstest_gen(x, unique=False, finite=False)[source]¶
Create a mappable function kstest to apply to each xmin in a list of xmins.
Parameters: unique : bool
If set, will filter the input array ‘x’ to its unique elements. Normally, this would be done at an earlier step, so unique can be disabled for performance improvement
finite : bool
Apply the finite-sample correction from Clauset et al 2007... Not clear yet which equation this comes from.
Docstring for the generated kstest function::
Given a sorted data set and a minimum, returns power law MLE ks-test against the data
data is passed as a keyword parameter so that it can be vectorized
The returned value is the “D” parameter in the ks test.
- plfit.plfit.most_likely_alpha(data, xmin, alpharange=(1.5, 3.5), n_alpha=201)[source]¶
Return the most likely alpha for the data given an xmin
- plfit.plfit.plexp_cdf(x, xmin=1, alpha=2.5, pl_only=False, exp_only=False)[source]¶
CDF(x) for the piecewise distribution exponential x<xmin, powerlaw x>=xmin This is the CDF version of the distributions drawn in fig 3.4a of Clauset et al. The constant “C” normalizes the PDF
- plfit.plfit.plexp_inv(P, xmin, alpha, guess=1.0)[source]¶
Inverse CDF for a piecewise PDF as defined in eqn. 3.10 of Clauset et al.
(previous version was incorrect and lead to weird discontinuities in the distribution function)
- class plfit.plfit.plfit(x, **kwargs)[source]¶
Bases: object
A Python implementation of the Matlab code `http://www.santafe.edu/~aaronc/powerlaws/plfit.m`_ from `http://www.santafe.edu/~aaronc/powerlaws/`_.
The output “alpha” is defined such that
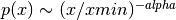
- alphavsks(autozoom=True, **kwargs)[source]¶
Plot alpha versus the ks value for derived alpha. This plot can be used as a diagnostic of whether you have derived the ‘best’ fit: if there are multiple local minima, your data set may be well suited to a broken powerlaw or a different function.
- discrete_best_alpha(alpharangemults=(0.9, 1.1), n_alpha=201, approximate=True, verbose=True, finite=True)[source]¶
Use the maximum likelihood to determine the most likely value of alpha
- alpharangemults [ 2-tuple ]
- Pair of values indicating multiplicative factors above and below the approximate alpha from the MLE alpha to use when determining the “exact” alpha (by directly maximizing the likelihood function)
- n_alpha [ int ]
- Number of alpha values to use when measuring. Larger number is more accurate.
- approximate [ bool ]
- If False, try to “zoom-in” around the MLE alpha and get the exact best alpha value within some range around the approximate best
vebose [ bool ] finite [ bool ]
Correction for finite data?
- lognormal(doprint=True)[source]¶
Use the maximum likelihood estimator for a lognormal distribution to produce the best-fit lognormal parameters
- plfit(nosmall=True, finite=False, quiet=False, silent=False, usefortran=False, usecy=False, xmin=None, verbose=False, discrete=None, discrete_approx=True, discrete_n_alpha=1000)[source]¶
A Python implementation of the Matlab code http://www.santafe.edu/~aaronc/powerlaws/plfit.m from http://www.santafe.edu/~aaronc/powerlaws/
See A. Clauset, C.R. Shalizi, and M.E.J. Newman, “Power-law distributions in empirical data” SIAM Review, 51, 661-703 (2009). (arXiv:0706.1062) http://arxiv.org/abs/0706.1062
There are 3 implementations of xmin estimation. The fortran version is fastest, the C (cython) version is ~10% slower, and the python version is ~3x slower than the fortran version. Also, the cython code suffers ~2% numerical error relative to the fortran and python for unknown reasons.
There is also a discrete version implemented in python - it is different from the continous version!
- discrete [ bool | None ]
- If discrete is None, the code will try to determine whether the data set is discrete or continous based on the uniqueness of the data; if your data set is continuous but you have any non-unique data points (e.g., flagged “bad” data), the “automatic” determination will fail. If discrete is True or False, the distcrete or continuous fitter will be used, respectively.
- xmin [ float / int ]
- If you specify xmin, the fitter will only determine alpha assuming the given xmin; the rest of the code (and most of the complexity) is determining an estimate for xmin and alpha.
- nosmall [ bool (True) ]
- When on, the code rejects low s/n points. WARNING: This option, which is on by default, may result in different answers than the original Matlab code and the “powerlaw” python package
- finite [ bool (False) ]
- There is a ‘finite-size bias’ to the estimator. The “alpha” the code measures is “alpha-hat” s.t. ᾶ = (nα-1)/(n-1), or α = (1 + ᾶ (n-1)) / n
- quiet [ bool (False) ]
- If False, delivers messages about what fitter is used and the fit results
- verbose [ bool (False) ]
- Deliver descriptive messages about the fit parameters (only if *quiet*==False)
- silent [ bool (False) ]
- If True, will print NO messages
- plotcdf(x=None, xmin=None, alpha=None, pointcolor='k', pointmarker='+', **kwargs)[source]¶
Plots CDF and powerlaw
- plotpdf(x=None, xmin=None, alpha=None, nbins=50, dolog=True, dnds=False, drawstyle='steps-post', histcolor='k', plcolor='r', **kwargs)[source]¶
Plots PDF and powerlaw.
kwargs is passed to pylab.hist and pylab.plot
- plotppf(x=None, xmin=None, alpha=None, dolog=True, **kwargs)[source]¶
Plots the power-law-predicted value on the Y-axis against the real values along the X-axis. Can be used as a diagnostic of the fit quality.
- test_pl(niter=1000.0, print_timing=False, **kwargs)[source]¶
Monte-Carlo test to determine whether distribution is consistent with a power law
Runs through niter iterations of a sample size identical to the input sample size.
Will randomly select values from the data < xmin. The number of values selected will be chosen from a uniform random distribution with p(<xmin) = n(<xmin)/n.
Once the sample is created, it is fit using above methods, then the best fit is used to compute a Kolmogorov-Smirnov statistic. The KS stat distribution is compared to the KS value for the fit to the actual data, and p = fraction of random ks values greater than the data ks value is computed. If p<.1, the data may be inconsistent with a powerlaw. A data set of n(>xmin)>100 is required to distinguish a PL from an exponential, and n(>xmin)>~300 is required to distinguish a log-normal distribution from a PL. For more details, see figure 4.1 and section
WARNING This can take a very long time to run! Execution time scales as niter * setsize
- plfit.plfit.plfit_lsq(x, y)[source]¶
Returns A and B in y=Ax^B http://mathworld.wolfram.com/LeastSquaresFittingPowerLaw.html
- plfit.plfit.test_fitter(xmin=1.0, alpha=2.5, niter=500, npts=1000, invcdf=<function plexp_inv at 0x7fced5360e60>)[source]¶
Tests the power-law fitter
Examples
Example (fig 3.4b in Clauset et al.):
xminin=[0.25,0.5,0.75,1,1.5,2,5,10,50,100] xmarr,af,ksv,nxarr = plfit.test_fitter(xmin=xminin,niter=1,npts=50000) loglog(xminin,xmarr.squeeze(),'x')
Example 2:
xminin=[0.25,0.5,0.75,1,1.5,2,5,10,50,100] xmarr,af,ksv,nxarr = plfit.test_fitter(xmin=xminin,niter=10,npts=1000) loglog(xminin,xmarr.mean(axis=0),'x')
Example 3:
xmarr,af,ksv,nxarr = plfit.test_fitter(xmin=1.0,niter=1000,npts=1000) hist(xmarr.squeeze()); # Test results: # mean(xmarr) = 0.70, median(xmarr)=0.65 std(xmarr)=0.20 # mean(af) = 2.51 median(af) = 2.49 std(af)=0.14 # biased distribution; far from correct value of xmin but close to correct alpha
Example 4:
xmarr,af,ksv,nxarr = plfit.test_fitter(xmin=1.0,niter=1000,npts=1000,invcdf=pl_inv) print("mean(xmarr): %0.2f median(xmarr): %0.2f std(xmarr): %0.2f" % (mean(xmarr),median(xmarr),std(xmarr))) print("mean(af): %0.2f median(af): %0.2f std(af): %0.2f" % (mean(af),median(af),std(af))) # mean(xmarr): 1.19 median(xmarr): 1.03 std(xmarr): 0.35 # mean(af): 2.51 median(af): 2.50 std(af): 0.07
plfit_py Module¶
Duplicate of the above plfit module, but without using numpy (or matplotlib, therefore no plots)
Pure-Python version of plfit.py¶
A pure python power-law distribution fitter based on code by Aaron Clauset. This is the slowest implementation, but has no dependencies.
Example very simple use:
from plfit_py import plfit
MyPL = plfit(mydata)
MyPL.plotpdf(log=True)
- plfit.plfit_py.plexp(x, xm=1, a=2.5)[source]¶
CDF(x) for the piecewise distribution exponential x<xmin, powerlaw x>=xmin This is the CDF version of the distributions drawn in fig 3.4a of Clauset et al.
- plfit.plfit_py.plexp_inv(P, xm, a)[source]¶
Inverse CDF for a piecewise PDF as defined in eqn. 3.10 of Clauset et al.
- class plfit.plfit_py.plfit(x, **kwargs)[source]¶
A Python implementation of the Matlab code http://www.santafe.edu/~aaronc/powerlaws/plfit.m from http://www.santafe.edu/~aaronc/powerlaws/
See A. Clauset, C.R. Shalizi, and M.E.J. Newman, “Power-law distributions in empirical data” SIAM Review, 51, 661-703 (2009). (arXiv:0706.1062) http://arxiv.org/abs/0706.1062
The output “alpha” is defined such that
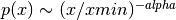
- alpha_(x)[source]¶
Create a mappable function alpha to apply to each xmin in a list of xmins. This is essentially the slow version of fplfit/cplfit, though I bet it could be speeded up with a clever use of parellel_map. Not intended to be used by users.
- plfit(nosmall=True, finite=False, quiet=False, silent=False, xmin=None, verbose=False)[source]¶
A pure-Python implementation of the Matlab code http://www.santafe.edu/~aaronc/powerlaws/plfit.m from http://www.santafe.edu/~aaronc/powerlaws/
See A. Clauset, C.R. Shalizi, and M.E.J. Newman, “Power-law distributions in empirical data” SIAM Review, 51, 661-703 (2009). (arXiv:0706.1062) http://arxiv.org/abs/0706.1062
nosmall is on by default; it rejects low s/n points can specify xmin to skip xmin estimation
This is only for continuous distributions; I have not implemented a pure-python discrete distribution fitter
- plfit.plfit_py.test_fitter(xmin=1.0, alpha=2.5, niter=500, npts=1000, invcdf=<function plexp_inv at 0x7fced51cc668>, quiet=True, silent=True)[source]¶
Tests the power-law fitter
Examples
Example (fig 3.4b in Clauset et al.):
xminin=[0.25,0.5,0.75,1,1.5,2,5,10,50,100] xmarr,af,ksv,nxarr = plfit.test_fitter(xmin=xminin,niter=1,npts=50000) loglog(xminin,xmarr.squeeze(),'x')
Example 2:
xminin=[0.25,0.5,0.75,1,1.5,2,5,10,50,100] xmarr,af,ksv,nxarr = plfit.test_fitter(xmin=xminin,niter=10,npts=1000) loglog(xminin,xmarr.mean(axis=0),'x')
Example 3:
xmarr,af,ksv,nxarr = plfit.test_fitter(xmin=1.0,niter=1000,npts=1000) hist(xmarr.squeeze()); # Test results: # mean(xmarr) = 0.70, median(xmarr)=0.65 std(xmarr)=0.20 # mean(af) = 2.51 median(af) = 2.49 std(af)=0.14 # biased distribution; far from correct value of xmin but close to correct alpha
Example 4:
xmarr,af,ksv,nxarr = plfit.test_fitter(xmin=1.0,niter=1000,npts=1000,invcdf=pl_inv) print("mean(xmarr): %0.2f median(xmarr): %0.2f std(xmarr): %0.2f" % (mean(xmarr),median(xmarr),std(xmarr))) print("mean(af): %0.2f median(af): %0.2f std(af): %0.2f" % (mean(af),median(af),std(af))) # mean(xmarr): 1.19 median(xmarr): 1.03 std(xmarr): 0.35 # mean(af): 2.51 median(af): 2.50 std(af): 0.07